Supponiamo ora, sempre continuando con il nostro esempio, di fare in modo che il numero prodotto in uscita dall'ADC vari da N ad N+1 quando la tensione di ingresso varia fra N*Q ed (N+1)Q.

Vedi esempio nella cartella Excel associata.

Vedi esempio nel documento associato.

Come si può notare, l'errore massimo che si commette, confrontando la tensione quantizzata con la tensione d'ingresso è proprio pari al quanto.

Vediamo ora un secondo esempio in cui facciamo in modo che l'uscita vari da N ad N+1 quando la tensione d'ingresso sia compresa a metà dell'intervallo compreso fra NQ ed (N+1)Q.

Vedi esempio nella cartella Excel associata.

Vedi esempio nel documento associato.

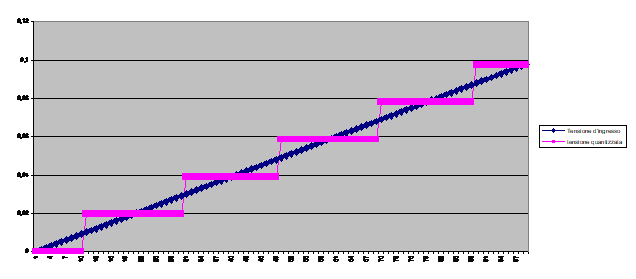
come si può verificare dal grafico e dai calcoli effettuati dal foglio elettronico si vede che l'errore massimo che si commette diventa la metà del quanto. Questa è la scelta ottimale, nel senso che permette di minimizzare l'errore di quantizzazione. . poiché con n bit si possono comporre al massimo 2ⁿ combinazioni diverse, il numero in uscita può essere al massimo 2ⁿ-1 corrispondente ad una tensione quantizzata V=Q*(2ⁿ-1). La tensione V_FS=Q*2ⁿ viene detta tensione di fondo scala. Nella migliore delle ipotesi l'errore di quantizzazione è pari a Q/2=(V_FS/2ⁿ⁾/2=V_FS/2ⁿ⁺¹.

L'errore di quantizzazione si può interpretare come un rumore indesiderato che si sovrappone al nostro segnale d'ingresso. Con una serie di passaggi matematici che non riportiamo per non rischiare di offendere le vostre meravigliose menti matematiche , degne di un Renato Caccioppoli, si trova che il rapporto fra il segnale e questo rumore diventa tanto migliore quanto maggiore è il rapporto fra il valore massimo del segnale ed il valore di fondo scala dell'ADC. Questo deriva dal fatto che un segnale di piccola ampiezza rispetto al valore di fondo scala dell'ADC non ne sfrutta tutta la risoluzione. Se dobbiamo convertire un segnale, quindi, conviene prima amplificarlo in modo da portare il suo valore massimo al massimo valore ammissibile in ingresso all'ADC. Dalla formula matematica che abbiamo tralasciato nonostante sapessimo di poter contare sulle vostre incredibili capacità matematiche universalmente riconosciute, si vede anche che il rapporto segnale-rumore migliora al crescere del numero n dei bit dell'ADC.

Il principio di funzionamento di un ADC è rappresentato in figura. Il blocco logica sequenziale è un blocco che è in grado di generare tutte le combinazioni possibili degli n bit dell'ADC. Queste sequenze di bit vanno in ingresso ad un DAC che genera la corrispondente tensione in uscita. Appena tale tensione diventa maggiore o uguale a quella di ingresso, l'uscita del comparatore va bassa bloccando il circuito sequenziale e congelando la stringa di bit che si voleva ottenere come risultato della conversione.

questo è lo schema di principio dei convertitori A/D a retroazione. L'esempio più semplice è il counting ADC o convertitore a conteggio o a gradinata i l cui schema di principio è il seguente

In questo ADC il circuito di logica sequenziale è un contatore binario, pilotato da un clock. Ad ogni impulso di clock il contenuto del contatore binario si aggiorna . il numero contenuto nel contatore passa al DAC. Quando la gradinata prodotta dal DAC raggiunge e supera il valore di tensione V_i, l'uscita del comparatore va a zero per cui blocca a zero l'uscita della porta AND, impedendo al clock di raggiungere il contatore binario. In tal modo l'uscita del contatore binario rimane congelata. Per far partire una nuova conversione occorre resettare il contatore binario mediante il segnale di RESET.

Questo tipo di convertitore presenta come problema fondamentale quello del tempo impiegato per la conversione che è elevato ed inoltre è molto variabile a seconda della tensione da convertire. Infatti tanto più è elevato il valore di tale tensione tanto maggiore sarà il numero di periodi di clock necessari perché l'uscita del DAC giunga a superare la tensione d'ingresso. Per sicurezza chi progetta il circuito in cui è inserito l'ADC, per evitare problemi di sincronizzazione dovrà considerare prudenzialmente il tempo massimo possibile che coincide con il tempo necessario affinché il contatore giunga a contare il numero massimo possibile che è 2ⁿ-1.

Servo-convertitore o tracking ADC o ADC ad inseguimento.

Se il segnale di ingresso diminuisce la sua ampiezza dopo che l'ADC ha portato a termine la sua conversione, il convertitore a gradinata non può modificare la sua uscita per seguire la diminuzione del segnale in ingresso. Per ottenere questa possibilità possiamo modificare lo schema precedente sostituendo al contatore up un contatore up/down facendo in modo che l'uscita del comparatore serva per selezionare la direzione del conteggio (vedi figura)

se la tensione d'ingresso è minore di quella fornita dal DAC, l'uscita del comparatore è a zero per cui il contatore funziona in modalità down e la tensione di uscita del DAC tende a diminuire. Se la tensione da convertire diventa superiore a quella del DAC, l'uscita del comparatore va ad 1 ed il contatore viene impostato in modalità up. Nella figura seguente è mostrato il processo di aggancio

se il convertitore è lasciato libero di inseguire le variazioni della tensione d'ingresso si dice che è in free running. Per questi tipi di convertitori non ha molto senso cercare di stabilire la velocità di conversione . diventa più interessante definire lo slew rate ammissibile in ingresso, cioè la velocità massima di variazione dell'ingresso affinché il convertitore sia ancora in grado di agganciarsi ad essa. Si può dimostrare che lo slew rate massimo è pari al rapporto fra quanto Q e tempo di clock.

Convertitori ad approssimazioni successive

Questa architettura consente di avere convertitori più veloci e quindi più adatti a sistemi di acquisizione dati basati su microprocessore.

il circuito sequenziale in questo caso è un registro S.A.R. o registro ad approssimazioni successive. Questo registro funziona nella logica della ricerca dicotomica. Applicata al nostro problema questa strategia si può rappresentare nel modo seguente. Noi vogliamo individuare la stringa di bit corrispondente al vaolroe di tensione V_i presente in ingresso. Consideriamo la seguente tabella che mostra le uscite del DAC per un ADC a 8 bit.

Data la tensione Vi d'ingresso si cerca di stabilire innanzitutto seil bit più significativo deve stare a 1 o a zero. Si pone il bit più significativo ad 1 e tutti gli altri bit a zero. Il DAC darà la tensione corrispondente e il comparatore confronterà le due tensioni. Se la tensione di uscita del DAC supera la tensione di ingresso da convertire il comparatore porta la sua uscita d 1 costringendo il SAR a porre l'MSB a 0. se la tensione di uscita del DAC è inferiore a quella di ingresso da convertire, il comparatore pone la sua uscita ad 1 lasciano il MSB del SAR ad 1. a questo punto il SAR pone il bit successivo (il bit 6) ad 1 e si esegue lo stesso controllo e così via fino a giungere a determinare il bit meno significativo. Supponiamo ad esempio di voler convertire una tensione d'ingresso pari a 4,2 volt. Il SAR pone l'MSB ad 1(il bit 7) e tutti gli altri bit a zero. Dalla tabella notiamo che ciò comporta una tensione in uscita dal DAC pari a 2,5 volt, per cui l'uscita del comparatore sarà 1. il SAR pone allora il bit 6 ad 1. dalla tabella vediamo che ciò corrisponde ad una tensione in uscita dal DAC pari a 3,75 volt. L'uscita del comparatore è ancora ad 1 per cui la scelta del bit 6 rimane inalterata. Ora il SAR prova a porre il bit 5 ad 1. ciò corrisponde ad una tensione in uscita dal DAC pari a 4,375 volt. Stavolta la tensione di uscita dal DAC è inferiore alla tensione che si vuole convertire per cui l'uscita del comparatore va a zero. Ne deriva che il SAR riporta il bit 5 a zero. Ora il SAR porta il bit 4 ad 1. ciò corrisponde alla stringa 11010000 e ad una tensione in uscita dal Dac pari a 4,0625 volt. Questa tensione è inferiore a quella d'ingresso per cui l'uscita del comparatore rimane a livello alto e il bit 4 rimane a livello logico 1. successivamente il SAR prova a porre il bit 3 a 1. la stringa 11011000 corrisponde ad una tensione in uscita dal Dac pari a 4,21875 volt. L'uscita del comparatore va bassa ed il bit verrà riportato a zero. Ciò avverrà anche per i bit 2,1 e 0. in definitiva il risultato della conversione sarà la stringa 11010000.

e' evidente il vantaggio in termini di tempi di conversione di un ADC ad approssimazioni successive rispetto ad un ADC a gradinata. Nel primo caso esso era pari a (2ⁿ-1)T_CK, ora è pari soltanto a (n-1)T_CK. vedremo più avanti che minore è il tempo di conversione e maggiore è la frequenza dei segnali che possiamo convertire.

Un esempio di realizzazione di un SAR è il seguente.

possiamo notare n flip flop di tipo JK ed un flip flop di controllo alla sinistra dello schema che decide se il clock di sistema può raggiungere o meno gli altri flip flop. Supponiamo di dare avvio alla conversione mediante il segnale SC (start of Convertion). Come si può vedere dallo schema, SC è collegato al segnale di Reset di ogni flip flop per cui resetta tutti i contatori e quindi il risultato dell'ultima conversione effettuata. Si noti che SC funge anche da segnale PE (Parallel Loading Enable) per lo shift register cioè consente che il registro venga caricato dai suoi ingressi. Ma i suoi inglesi sono bloccati in modo che il bit meno significativo venga posto ad 1 e gli altri a 0. in sostanza i flip flop vengono azzerati e lo shift register viene caricato con la stringa 00000001. poiché il flip flop di controllo è stato resettato la sua uscita Q si porta a zero e viene usata come si può vedere dallo schema per generare un segnale BUSY attivo basso che indica, finché sta a zero, che l'ADC è impegnato nella conversione. L'uscita Q negata sta invece ad 1 e, costituendo uno degli ingressi di una porta AND consente al clock di sistema di raggiungere gli altri flip flop e lo shift register. Ora consideriamo il flip flop più significativo: J si trova ad 1 perché corrisponde al bit meno significativo in uscita dello shift register, mentre come si può notare dallo schema K è pari a 0. allora b_n-1=1 e gli altri bit si portano a zero. Ad un nuovo ciclo di clock viene attivato lo shift register per cui il bit 1 passa da T₀ a T_1. per cui per il flip flop corrispondente al bit b_n-2 J=1 e K=0, allora b_n-2 viene portato ad 1. intanto il DAC ha provveduto a generare la tensione corrispondente alla stringa 10000000. ora se tale tensione risulta superiore a V_i, l'uscita del comparatore si trova ad 1, per cui C=1, allora per il flip flop corrispondente al bit b_n-1 si ha che J=0 perché corrisponde a T₀ che per effetto dello shift è diventato 0, mentre K è il risultato della AND fra T₁ che adesso è pari ad 1 per effetto dello shift e di C=!,. l'uscita della And è allora pari a 1 per cui J=0 e K=1 e il flip flop viene resettato per cui b_n-1 torna a zero. se invece la tensione V_R, corrispondente alla stringa 10000000, è inferiore alla tensione V_i, si ha C=0, l'uscita della AND =0, per cui J=0, K==, e il flip flop resta nelo stato precedente. Abbiamo dunque fatto in modo di variare automaticamente il valore del bit più significativo. Via via che i vari impulsi di clock fatto shiftare l'uno nello shift register lo stesso processo avverrà per ogni flip flop, per cui i vari bit verranno settati o resettati automaticamente. Quando il bit di controllo raggiunge il bit T_n, poiché questo è collegato all'ingresso J del flip flop di controllo tale flip flop viene settato, l'uscita BUSY torna ad 1 ad indicare che la conversione è terminata, la sua uscita Q negata va a zero ed il clock non si può più propagare al SAR bloccando la conversione.

IL convertitore parallelo o flash

La struttura di un convertitore parallelo è la seguente

come si può vedere dalla figura abbiamo una batteria di comparatori di tensione. La tensione da convertire viene mandata in parallelo a tutti i comparatori. Ogni comparatore la confronterà con una tensione di riferimento ottenuta da un partitore resistivo. Come si può notare dalla figura si vuole fare in modo che le transizioni dei bit avvengano a metà dell'intervallo di quantizzazione.

La rete di decodifica trasforma le uscite dei comparatori in codice binario. E' evidente che un sistema di questo tipo è il più veloce immaginabile. Il difetto è dato dal fatto che all'aumentare dei bit del ADC la complessità del circuito aumenta in maniera proibitiva. Se , ad esempio, vogliamo realizzare un DAC ad 8 bit, le combinazioni possibili, cioè il numero dei livelli di discretizzazione è pari a 2⁸=256, per cui occorrerebbero 256 comparatori diversi.

Parametri e cause di errore in un ADC.

Codici mancanti

Questa possibile causa di errore si può verificare nel caso di ADC a contrazione che contengono un DAC al proprio interno. Questo errore deriva da un errore di non linearità del DAC.

a causa della non linearità del DAC (vedi figura), si ha un codice mancante, infatti se, in corrispondenza di quel codice il DAC fornisce in uscita il livello corrispondente ad un altro codice, il blocco di logica sequenziale non potrà riprodurlo in uscita.

Transizione di zero

Abbiamo visto che, allo scopo di minimizzare l'errore introdotto dalla quantizzazione si cerca di fare in modo che la transizione da una combinazione di bit ad un'altra avvenga a metà di un intervallo di quantizzazione. L'offset del comparatore o errori di zero del DAC possono fare in modo che ci sia una traslazione nel punto di transizione.

Errore di guadagno, di non linearità e di non linearità differenziale

Sono errori causati dagli errori omologhi del DAC.